In this article we will look at electrical formula for calculating resistance. The reason why I emphasize “electrical” formula is because there is also “physical” formula for calculating resistance. The formula is shown to the left.
In general, resistance opposes flow of current. This equation actually comes from Ohm’s Law when we solve it by R.
In this equation, resistance is designated with letter R and it is expressed in Ω’s (Ohms). Letter V is used for voltage. The unit for voltage is: Volt. Letter I is used for current. The unit for current is: Ampere or Amp for short.
It is important to note that voltage V is voltage across the resistor, while current I is the current that flows through the resistor.

In this formula, resistance is directly proportional to voltage. That means that: the larger the voltage, the larger the resistance. Also, resistance is inversely proportional to current. Thus: the larger the current, the smaller the resistance.
Resistance can be a property of a piece of wire, or a conductor, an element in the circuit, for example resistor, or a whole circuit or a network of elements. In Electrical Circuits Theory, we will sometimes use expression “input resistance” or “output resistance” of a circuit.
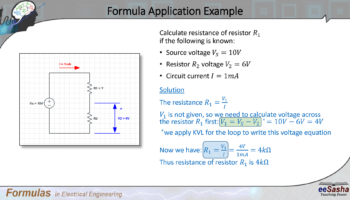
Here is one example of application of the formula for calculating resistance.
Problem statement
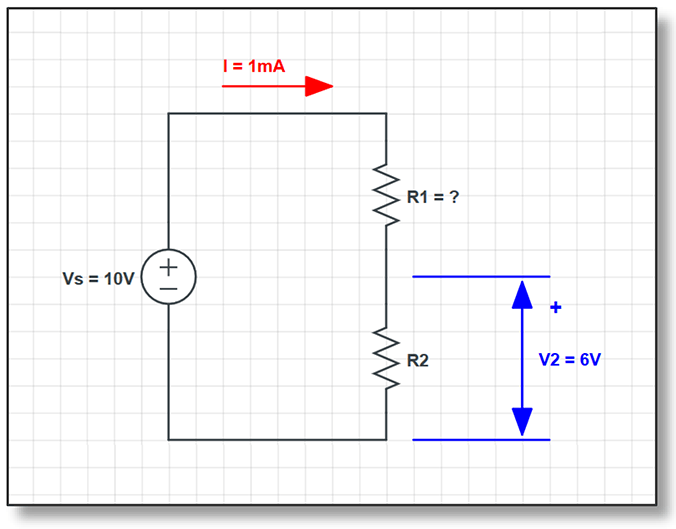
Calculate resistance of resistor R1 if the following is known:
- The source voltage Vs is 10V
- The resistor R2 voltage V2 is 6V
- The circuit current I is 1mA
Solution
In order to find the resistance, we need to apply the formula: R1=V1/I. However, V1 is not given, so we need to calculate voltage across the resistor R1 first. If we apply KVL or Kirchhoff’s Voltage Law for the loop in this circuit, we can write the following voltage equation: V1=Vs-V2. Thus V1 is 10V-6V, which is 4V.
Now we have everything we need to calculate the resistance R1. So R1 is V1/I, which is 4V/1mA, which gives us 4kΩ. Thus the resistance of resistor R1 is 4kΩ.
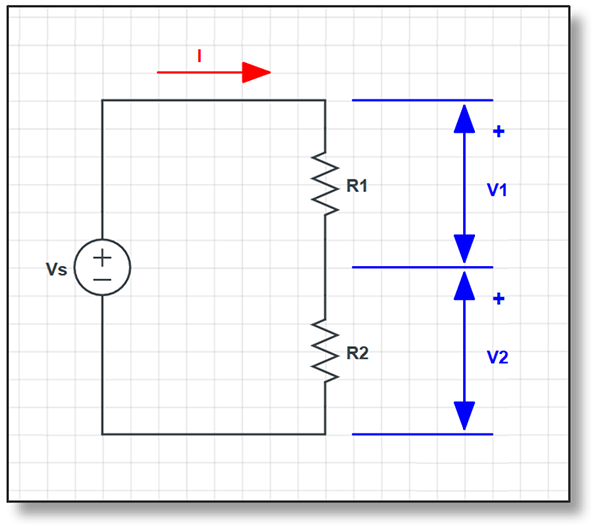
Even though the formula for calculating resistance is very simple, students sometimes make mistakes.
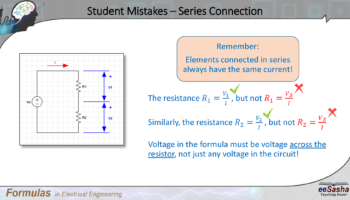
Here we have an example of a series circuit. In a series circuit, all elements are connected in series.
So in order to calculate resistance R1, we need to divide voltage V1 with current I. The mistake is to divide voltage Vs with the current I. Similarly, the resistance R2 is V2 divided by I, but not Vs divided by I.
Thus remember, voltage in the formula must be voltage across the resistor, not just any voltage in the circuit. Just because current is same for all the elements connected in series, it doesn’t mean that their voltages are the same.
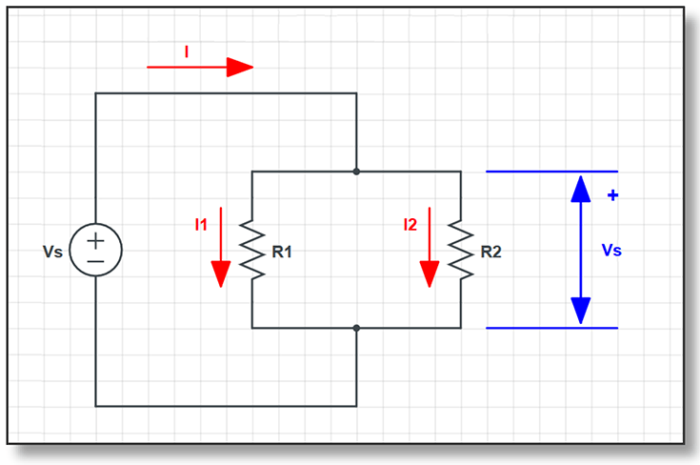
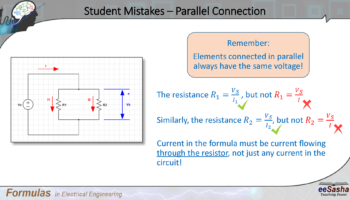
Here is similar but opposite example where students also tend to make mistakes. This particular circuit is a parallel connection of two resistors.
In parallel connection, elements don’t necessarily have the same currents, so we need to use corresponding current when we calculate the resistance. Thus the resistance R1 is Vs divided by I1, but not Vs divided by I. Similarly, the resistance R2 is Vs divided by I2. So we cannot calculate R2 as Vs over I.
Thus the current that we use in this formula must be current flowing through the resistor, not just an arbitrary current in the circuit.
I hope you liked this Formula article and you learned something new today. If you prefer watching videos, here is the video for you.
I am constantly developing new courses that go into much more depth in all of these topics. Thank you for stopping by and see you soon!
Below you can find all the slides I used to develop this blog post and the video: