During their normal course of a life, batteries go through many cycles of being charged and discharged. One cycle consists of a process of first charging a battery and then discharging it. The whole purpose of charging a battery is so it can store electric energy and later perform some useful work with it, during which the battery gets discharged.
We can assume that the battery is empty at the beginning of a cycle. Then it gets fully charged and ultimately fully discharged. The cycle ends at the same “level of charge” as it was at the beginning of a cycle – in this case: an empty battery.
The amount of charge contained in a battery is described by its State of Charge (SOC). The state of charge can take any value between 0% (battery empty) and 100% (battery fully charged). Thus, we can describe battery cycle as change in its state of charge:
- Charging – SOC increases from 0% to 100%
- Discharging – SOC decreases from 100% to 0%
In reality, batteries are never fully discharged. In fact, some batteries can get damaged by excessive discharge and SOC should never drop below a certain level (say 20%). Thus the cycle can also be considered as SOC raising from, say 20% to 100% and then dropping back to 20%, which completes the cycle. It actually gets more complicated as the level of discharge (or even both level of discharge and level of charge) vary from cycle to cycle.
When we supply electrical energy to the battery, the battery gets charged. The electrical energy gets converted inside the battery into a chemical energy. This process of conversion is inevitably associated with energy losses. It is probably the easiest to think of these losses as heat dissipated from the battery during the charging process.
We can designate electrical energy supplied to the battery as: Wsupplied
Chemical energy ultimately stored inside the battery is: Wstored
The difference is the energy lost in the conversion process: Wcharging losses
Obviously, due to energy losses, the energy supplied is larger than the energy stored:
Wsupplied > Wstored
As a matter of fact, the following equation holds:
Wsupplied – Wcharging losses = Wstored
These relationships are represented on the following diagram:
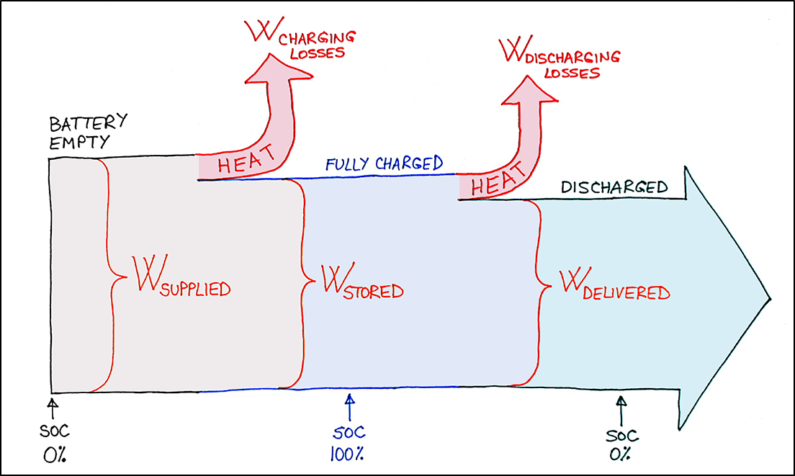
An opposite process to charging is discharging of a battery. Now the energy flows in an opposite direction: Chemical energy stored inside the battery gets converted into an electrical energy that is delivered by the battery to an external electrical circuit.
The process of conversion is again followed by energy losses and we can again think of these losses as heat dissipated from the battery. You may have experienced working on your laptop while holding it on your lap, and the laptop eventually becoming too hot to keep it on the lap! It is not really the laptop that gets hot, but the battery inside it (as it powers the laptop).
For discharging process, we start from chemical energy stored inside the battery: Wstored
Electrical energy delivered by the battery is: Wdelivered
And again, the difference is the energy lost in the conversion process: Wdischarging losses
Once more, due to energy losses, the energy stored is larger than the energy delivered:
Wstored > Wdelivered
Which, more precisely, can be described by the following energy equation:
Wstored – Wdischarging losses = Wdelivered
Within one cycle, energy flows into the battery during charging and it flows out of the battery while battery discharges. The State of Charge (SOC) changes from 0% to 100% and back to 0%. Heat is dissipated all along, whenever SOC changes, whether it increases or decreases.
The cycle of charging and discharging is associated with three distinct energies: Wsupplied, Wstored and Wdelivered. If we know all three of these energies, we can express separate efficiencies of charging and discharging processes by the following two equations:

When losses are involved, the efficiency must be smaller than 100%. Perfect 100% efficiency can only be achieved in ideal scenarios. In reality, most (if not all) processes are inherently associated with losses and consequently have less than ideal efficiency. The only question is: How much lower than 100% will the efficiency be?
As stated above, Wstored < Wsupplied and consequently ηchg < 1.
Similarly, Wdelivered < Wstored and thus the discharging efficiency ηdis chg < 1.
Both efficiencies are smaller than 1 due to inevitable losses. The actual amount of energy lost in the process of charging or discharging determines the value of corresponding efficiency.
Considering that chemical energy Wstored is hard to measure, it is difficult to determine individual charging and discharging efficiencies ηchg and ηdis chg. However, the efficiency of an entire cycle can be calculated based only on electrical energies Wsupplied and Wdelivered:
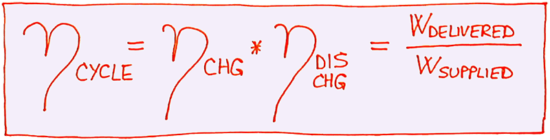
Electrical energy is easy to measure, which makes it easy to determine efficiency of a full battery cycle ηcycle. Again, since Wdelivered < Wsupplied then ηcycle < 1. However, note that efficiency of a full cycle comprises both charging and discharging losses and consequently efficiency of a full cycle is even smaller than either of individual charging or discharging efficiency:
ηcycle < ηchg and ηcycle < ηdis chg
Mathematically, this is easy to prove. Since both ηchg < 1 and ηdis chg < 1, their product ηcycle must be even smaller. For example, if both charging and discharging efficiencies are 90%, then the overall efficiency is ηcycle = 0.9 • 0.9 = 0.81 = 81% < 90%.
Charging and discharging efficiencies are not necessarily equal, but roughly saying, they can be estimated as the same. Since the efficiency of a full battery cycle ηcycle is easy to determine, we can indirectly easily calculate individual charging and discharging efficiencies as a square root of efficiency of the entire cycle:
ηchg ≈ ηdis chg ≈ √(ηcycle)
Keep in mind that all efficiencies in the equation above must be actual numbers smaller than 1 and not percentage numbers. Thus this is correct: ηchg ≈ √(0.81) = 0.9. Do not use percentage numbers, i.e ηchg ≠ √(81) = 9 as this makes no sense.
We can determine capacity of a battery CA based on the amount of charge we put into the battery during the process of charging. We can also measure the amount of charge obtained from the battery during the process of discharging. However, it is important to realize that we make many assumptions along the way and the obtained capacity is only an approximate value:
- We assume the number of electrons in and electrons out must be the same. That may only be true in a perfectly reversible chemical process. No chemical process is perfectly reversible and some electrons get “captured” and we may never get them back out of the battery. Consequently, charging and discharging capacity is not the same
- We do not count the electrons. We calculate the amount of charge based on measuring current and time. Both are prone to errors. Consequently, the calculated capacity will not be perfectly accurate
- We assume that charging or discharging current is constant in time so we can apply simple formula to calculate the amount of charge (CA = Q = I • t). This formula is only approximate and when current varies, it needs to be integrated in time to obtain the accurate charge that flows in or out of the battery. Thus the obtained capacity is only approximate
- Similarly, we assume that voltage during charging or discharging is constant in time so we can apply simple formula to calculate the energy (CW = W = V • I • t). However, voltage inevitably varies and energy calculated is not very precise. Furthermore, the average charging voltage and the average discharging voltage have different values
It is clear that accuracy of battery’s capacity (whether CA or CW) is only as good as much we are able to overcome the assumptions listed above. And of course, keep in mind that due to losses (or battery cycle efficiency being smaller than 100%), the discharge capacity will be closer to what you can expect from the battery when you actually put it to work!
For practical purposes, always assume that capacity of a battery will be smaller than what is stated by the manufacturer. Also note that how slowly or quickly battery charges or discharges, plays a vital role in the efficiency of a chemical process inside the battery. On top of that, the ambient temperature affects the process of energy conversion and consequently affects the capacity as well.


